Diferenças entre edições de "Teste/math"
(Criou a página com "Algum texto final. Categoria:Teste") |
|||
| (Há 12 edições intermédias do mesmo utilizador que não estão a ser apresentadas) | |||
| Linha 1: | Linha 1: | ||
<nowiki>$\newcommand{\Re}{\mathrm{Re}\,} |
|||
\newcommand{\pFq}[5]{{}_{#1}\mathrm{F}_{#2} \left( \genfrac{}{}{0pt}{}{#3}{#4} \bigg| {#5} \right)}$ |
|||
Teste onde <math>x</math> é definido por:</nowiki> |
|||
<math>\begin{align} |
|||
\dot{x} & = \sigma(y-x) \label{eq:1}\\ |
|||
\dot{y} & = \rho x - y - xz \\ |
|||
\dot{z} & = -\beta z + xy |
|||
\end{align}</math> |
|||
Equation \eqref{eq:1} above. |
|||
\begin{equation} |
|||
\label{eq:aa} |
|||
x = y^2 |
|||
\end{equation} |
|||
Equation \eqref{eq:2} here. |
|||
We consider, for various values of $s$, the $n$-dimensional integral |
|||
which occurs in the theory of uniform random walk integrals in the plane, |
|||
where at each step a unit-step is taken in a random direction. As such, |
|||
the integral \eqref{def:Wns} expresses the $s$-th moment of the distance |
|||
to the origin after $n$ steps. |
|||
===Secção adicional=== |
|||
By experimentation and some sketchy arguments we quickly conjectured. Insert picture: |
|||
[[Ficheiro:Cat2.jpg|alt=Gato deitado|miniaturadaimagem|Legenda da imagem.]] |
|||
strongly believed that, for $k$ a nonnegative integer |
|||
\begin{equation} |
|||
\label{eq:W3k} |
|||
W_3(k) = \Re \, \pFq32{\frac12, -\frac k2, -\frac k2}{1, 1}{4}. |
|||
\end{equation} |
|||
Appropriately defined, \eqref{eq:W3k} also holds for negative odd integers. |
|||
The reason for \eqref{eq:W3k} was long a mystery, but it will be explained |
|||
at the end of the paper. |
|||
$\ce{HCl}$ dissociates in water as follows: |
|||
$$\ce{H2O + HCl <=> H3O+ + Cl-}$$. |
|||
A equação que define $x$ é a seguinte, onde $x = a^2 + b_2$: |
|||
\[ |
|||
x = \frac{a+b}{c} + \sum_{i=1}^{n} B_i \alpha \beta \gamma \phi_k |
|||
\] |
|||
Uma frase de teste<ref>'''J. Pinto''', ''Livro de texto'', Coimbra Editora (2017).</ref>. Uma ligação a [[wikipedia:Process_integration|integração de processos]]. |
|||
Mais referências.<ref>'''I.C. Kemp''', ''Pinch Analysis and Process Integration, A User Guide on Process Integration for the Efficient Use of Energy'', 2.a edição, Butterworth-Heinemann, Amsterdam, (2007).</ref> |
|||
Bibliografia recomendada: |
|||
<references /> |
|||
Algum texto final. |
Algum texto final. |
||
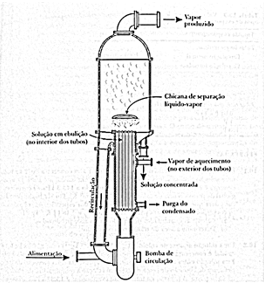
[[Ficheiro:Figura 10..png|alt=Evaporador|miniaturadaimagem|Legenda por baixo.|nenhum]] |
|||
<br /> |
|||
[[Categoria:Teste]] |
[[Categoria:Teste]] |
||
Edição atual desde as 23h30min de 17 de abril de 2019
$\newcommand{\Re}{\mathrm{Re}\,} \newcommand{\pFq}[5]{{}_{#1}\mathrm{F}_{#2} \left( \genfrac{}{}{0pt}{}{#3}{#4} \bigg| {#5} \right)}$ Teste onde <math>x</math> é definido por:
Falhou a verificação gramatical (função desconhecida: "\label"): {\displaystyle \begin{align} \dot{x} & = \sigma(y-x) \label{eq:1}\\ \dot{y} & = \rho x - y - xz \\ \dot{z} & = -\beta z + xy \end{align}}
Equation \eqref{eq:1} above. \begin{equation} \label{eq:aa} x = y^2 \end{equation} Equation \eqref{eq:2} here.
We consider, for various values of $s$, the $n$-dimensional integral which occurs in the theory of uniform random walk integrals in the plane, where at each step a unit-step is taken in a random direction. As such, the integral \eqref{def:Wns} expresses the $s$-th moment of the distance to the origin after $n$ steps.
Secção adicional
By experimentation and some sketchy arguments we quickly conjectured. Insert picture:
strongly believed that, for $k$ a nonnegative integer
\begin{equation}
\label{eq:W3k}
W_3(k) = \Re \, \pFq32{\frac12, -\frac k2, -\frac k2}{1, 1}{4}.
\end{equation} Appropriately defined, \eqref{eq:W3k} also holds for negative odd integers. The reason for \eqref{eq:W3k} was long a mystery, but it will be explained at the end of the paper.
$\ce{HCl}$ dissociates in water as follows: $$\ce{H2O + HCl <=> H3O+ + Cl-}$$.
A equação que define $x$ é a seguinte, onde $x = a^2 + b_2$: \[ x = \frac{a+b}{c} + \sum_{i=1}^{n} B_i \alpha \beta \gamma \phi_k \]
Uma frase de teste[1]. Uma ligação a integração de processos. Mais referências.[2]
Bibliografia recomendada:
Algum texto final.